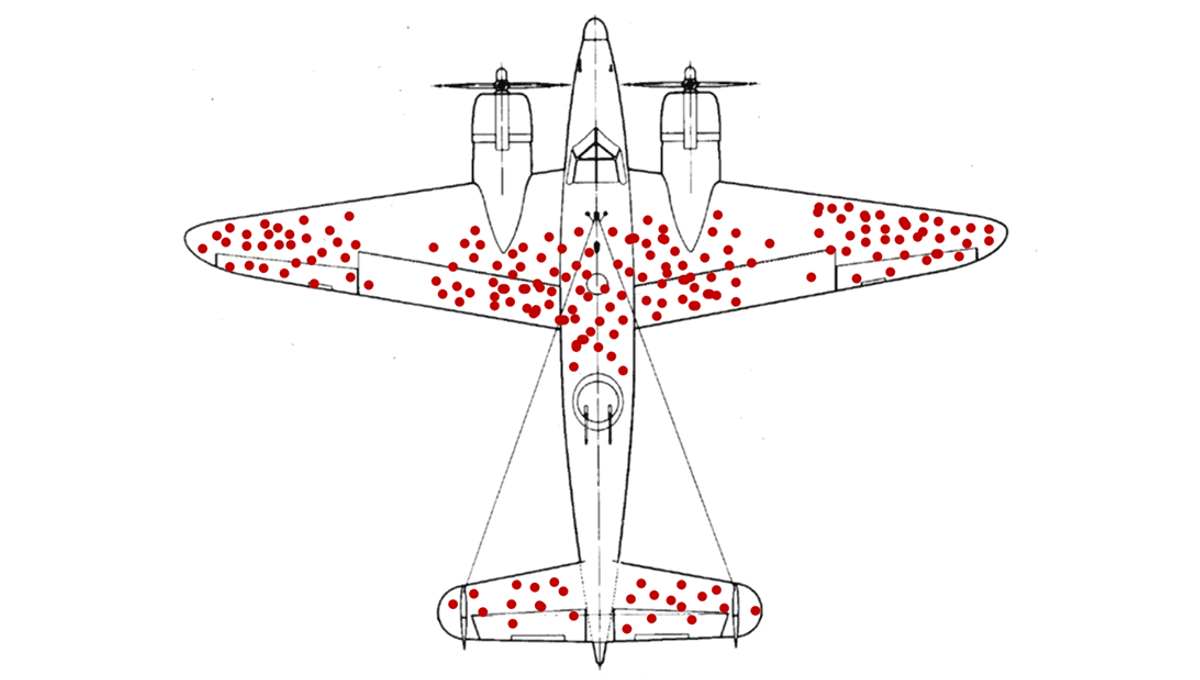
Das ist simuliert für den Fall, dass jeder der vier Spieler eine andere Zahl wählt.
Erst mal vielen Dank für deine Simulation! Spannend wäre nun noch eine zweite Simulation für den Fall, dass alle vier Helden dieselbe Zahl wählen, und dann ein direkter Vergleich der beiden Simulationen nebeneinander. Vielleicht findest du dazu ja auch noch mal die Zeit!? Das wäre super duper lieb!
![]()
![]()